


|
| 1 Horror Vacui 2 A Very Patient Turtle Who Draws Lines 3 A Taxonomy of Fractology 4 Gallery of Specimens |
| Root 2 Family | Root 3 Family | Root 4 Square Grid Family | Root 4 Triangle Grid Family |
| Root 5 Family | No Root 6! | Root 7 Family | Root 8 Family |
| Root 9 Square Grid Family | Root 9 Triangle Grid Family | Root 10 Family | Root 12 Family |
| Root 13 Square Grid Family | Root 13 Triangle Grid Family | Root 16 Square Grid Family | Root 16 Triangle Grid Family |
| Root 17 and Beyond... | 5 My Brain Fillith Over | 6 References | 7 Acknowledgements |

|
1. Horror Vacui
|
| There is a concept in visual art known as: horror vacui : "fear of empty space", illustrated by many art styles throughout history. The specimens in this book have a major case of horror vacui: they are truly haters of empty space! A similar concept is found in physics: the notion that "nature abhors a vacuum." Fractal curves are very rich in metaphorical power - providing models for art, physics, music, and biology. They even evoke philosophical concepts, such as how the paths of our lives are repetitive, and filled with theme and variation - at every time scale. |
|
Our Mascot
How could I not mention brain coral in a book called, "Brain-filling Curves"? Well, I will mention it now! This curious undersea creature - a coral of the family Faviidae - is covered with wonderful curly mazes. Hats off to this inspiring creature. |

|
|
Certain animals - especially really long skinny ones - sometimes find the need to coil themselves up to take up a compact space. We humans also happen to have about seven meters of intestine packed tightly into our abdomens: that's quite a spacefiller!
Any time you have a long flexible linear object, and a desire to have that object take up a small space, you enter into a special realm of geometrical problem-solving - a realm that involves twisting, turning, bending, folding, and wrapping. |

|
| This geometric realm is also invoked for the purpose of creating convoluted paths to follow, like a maze or a labyrinth. |

|
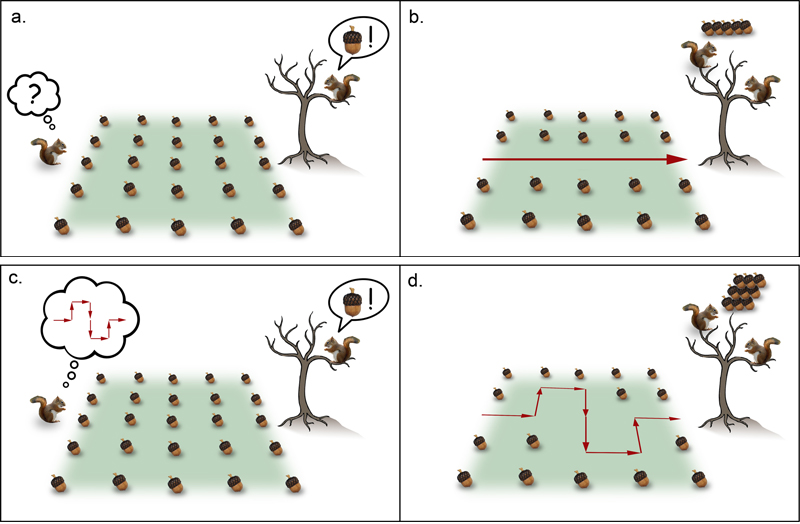
| Convoluted paths are also created when animals forage, or seek out things in the environment. Let's do a visual thought experiment: imagine that you are a squirrel, scurrying around on the ground under a tree. Your mate is up in the tree, and she asks you to collect as many acorns as you can, and bring them up to her...in a hurry. |
| You think to yourself, "well, I could go straight to the tree and collect all the acorns in my path. That would get me to my mate quickly, but I may not collect many acorns." This is illustrated on the next page in panel (b). Just as you feared, when you arrive, your mate complains: "only five acorns?" You confess that there were only five acorns in your immediate path, and you grabbed them all up. The next day your mate asks you again to come back home to the tree and to bring back as many acorns as you can. This time you decide to take a few diversions on your way to the tree (one diversion to the left, and one diversion to the right). These diversions yield four more acorns, as illustrated in panel (d). |

|
|
If you feel that you have a little more time on your hands (or rather, your paws), you might decide to make smaller diversions inside of your diversions - to grab up even more acorns. This is illustrated at the bottom of the page. These smaller diversions have the same shape as the bigger ones, but they are on a smaller scale.
The result of this visual thought experiment is a two-level fractal curve - a curve that may look familiar to some of you: it is the boundary of the quadric Koch Island [15]. The visual diagram that the squirrel conjured up in panel (c.) is the "generator" for this fractal curve. The concept of generators will be explained in the next chapter. |
|

|
The diagram at left shows how the paths that make up the squirrel's left-right diversions each have their own miniature left-right diversions.
Now, you may ask: why doesn't our make-believe squirrel just scan the whole field of acorns one row at a time? 
Well, that's a valid way to collect a field full of acorns, but it's boring! (Our squirrel has a fractal mind.) |
| How many ways can you draw a curly line? |

|
|
Infinite Strings
Imagine taking a piece of string, and coiling it up so that it takes up a small space. The picture at the right shows a string with black dots drawn at the endpoints. As we move these dots closer to each other, we allow the string to curl up. Imagine that our task is to make sure the string never touches itself or crosses over itself, even as we push the endpoints closer and closer to each other. Eventually of course, the string will get packed so tightly that it will have to touch itself. But that's only because physical strings have thickness. This book is not about mortal pieces of string that reside in our physical world. It is about Platonic pieces of string. A perfect geometrical curve is infinitely thin, and so it can keep coiling up as the ends get closer together - essentially forever...and it will never touch itself. But that's no fun. After all, the end result of this process would be a blob of string so small that it would basically be a point. And it is well established in science that infinitely small things like points are extremely difficult to see. |

|

|
So instead let's imagine that we keep the endpoints the same distance from each other, and that the string gets longer and longer, adding more and more bays and peninsulas to fill up space. This is illustrated below. I use the term "fractalize" to describe this process. It turns out that there are many ways that a curve can be fractalized as it gets longer. And we can capture some of these ways in simple, elegant geometrical processes.
The art of discovering these processes, and the categorization of these curves, is the subject of this book. |

|
| The drawing below shows one of the many fractal curves I have discovered. The two ends of the line are shown with black dots, visible at the lower left and lower right. Because of the particular scheme this fractal curve uses to fill space, there are unique self-similar patterns distributed throughout. The explanation for this phenomenon is explained later, as well as the genetic code used to generate this particular specimen. |

|
|
Filling-in the Gaps
A fractal curve that doesn't cross itself can be described as the boundary between two highly-intertwined domains. Like sea and land, or like lungs and air, these boundaries can be highly convoluted. Let's take the fractal curve from the previous page, and fill it up with light-blue water, to see what happens... |

|
| The curly lines have receded to the background and what we see instead are two domains: one white, and one light blue. If this were a map of canals in a seaside village, you would use this to determine a route to paddle your gondola from one part of the village to another. As a general rule, I prefer to let the beauty of the curve itself shine through, but in many cases, the shapes between the curves are just as interesting. You will see that I use this colorizing technique for many of the fractal images in this book. |
|
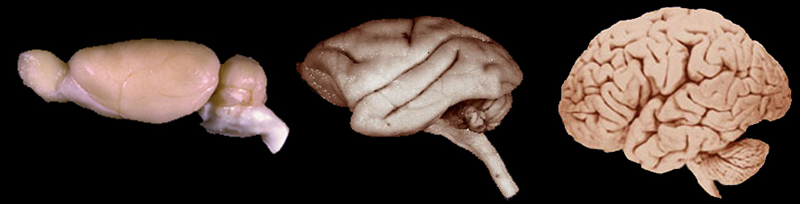
Filling Your Brain
The evolution of brain folds is roughly correlated with advances in animal intelligence. Here are three brains for your viewing pleasure: from left to right: rat, monkey, and human (these images have been scaled relative to each other). |
|
| I would like this book to cause a few more folds to grow in your brain. And I would like that growth to be joyful. Curves that completely fill up a region of a plane are called "plane-filling curves". They are familiar to fractal-lovers: mathematicians, geometers, and artists of the Escher ilk. For many of us, the reason we love these curves is not because they answer questions like how to pack leftover spaghetti into a jar, or how to build a maze for your pet rat. The reason is because we find them beautiful - visually and intellectually. |

|
| Although these kinds of curves have been created in the past, they were generally considered as mathematical curiosities, or worse, "monsters" until, in the 1970's, Benoit Mandelbrot coined the term "fractal" and brought together many of these beasts under one umbrella; as a unified mathematical discipline. In his book, The Fractal Geometry of Nature [14], Mandelbrot referred to plane-filling curves as "Peano Curves", in reference to Guiseppe Peano, an Italian mathematician who described such curves in the 1890's [18]. Mandelbrot's book is the foundation for many of the concepts and terms I use in this book. But I shall extend these ideas and terms, and put them in a new context - a context in which plane-filling fractal curves can be explored without end - and with beautiful results. |
|
A Definition
Now is a good time to give a more formal, more general definition: a "space-filling curve" can be described as a continuous mapping from a lower-dimensional space into a higher-dimensional space. In traditional mathematics, a curve is described as a topological space that is homeomorphic to a line: if you magnify a small region of the curve, it looks like a straight line. The higher the magnification, the more it looks like a straight line. But...fractals came along and changed all that! Consider a curvy line that has an infinite number of curls, bends and folds...at every level of magnification. And consider a curve that has such a serious case of horror vacui that it visits every point in a planar area in its path from start to finish. This is what we mean by a "plane-filling curve". It is the topological equivalent to a planar shape covering that same region. So you can think of this curve as being a particular way to describe that planar shape. In other words, it provides a mapping between a line and a 2D shape. Mandelbrot used the term "sweep" to distinguish a plane-filling curve from any old 2D planar shape, implying the progression of a path that passes through every point in that shape over some period of time. (A more thorough overview of space-filling curves is given by Hans Sagan [20]). |
| I have been exploring fractal curves now for about twenty-five years, and I have drawn several hundred pictures (probably more than a thousand), in my lifelong search for fractal curves. I have also developed genetic algorithms and other computational search techniques to find new specimens. This book shows the culmination of my search for plane-filling curves. I have accumulated over 200 specimens and organized them according to a taxonomy of fractal curve families. Each specimen is shown with a unique genetic code. And I have included several color images of what I consider to be the most striking specimens. Many of these - I have reason to believe - have never been seen before, and I am delighted to introduce them to you. |

|

|
| 1 Horror Vacui 2 A Very Patient Turtle Who Draws Lines 3 A Taxonomy of Fractology 4 Gallery of Specimens |
| Root 2 Family | Root 3 Family | Root 4 Square Grid Family | Root 4 Triangle Grid Family |
| Root 5 Family | No Root 6! | Root 7 Family | Root 8 Family |
| Root 9 Square Grid Family | Root 9 Triangle Grid Family | Root 10 Family | Root 12 Family |
| Root 13 Square Grid Family | Root 13 Triangle Grid Family | Root 16 Square Grid Family | Root 16 Triangle Grid Family |
| Root 17 and Beyond... | 5 My Brain Fillith Over | 6 References | 7 Acknowledgements |


|
Brain-filling Curves - A Fractal Bestiary
by Jeffrey Ventrella Distributed by Lulu.com Cover Design by Jeffrey Ventrella |
Book web site:
BrainFillingCurves.com
ISBN 978-0-9830546-2-7 Copyright © 2012 by Jeffrey Ventrella |

eyebrainbooks.com |

FractalCurves.com |