E(2,1) norm 3 family

This family corresponds to an Eisenstein integer with norm 3. Since it is a prime, all generator integers have norm 1. There are two generator shapes in this family. Two of the curves are self-avoiding.

name: Terdragon reference: Larry Riddle comment: Palindrome curve (point-symmetry)

name: Inverted Terdragon reference: fractalcurves.com comment: Different skin than the Terdragon

name: Half-Terdragon reference: Tom Karzes' fractal page comment:

name: Walking Terdragon reference: The Family Tree of Fractal Curves comment: This is a self-avoiding curve.

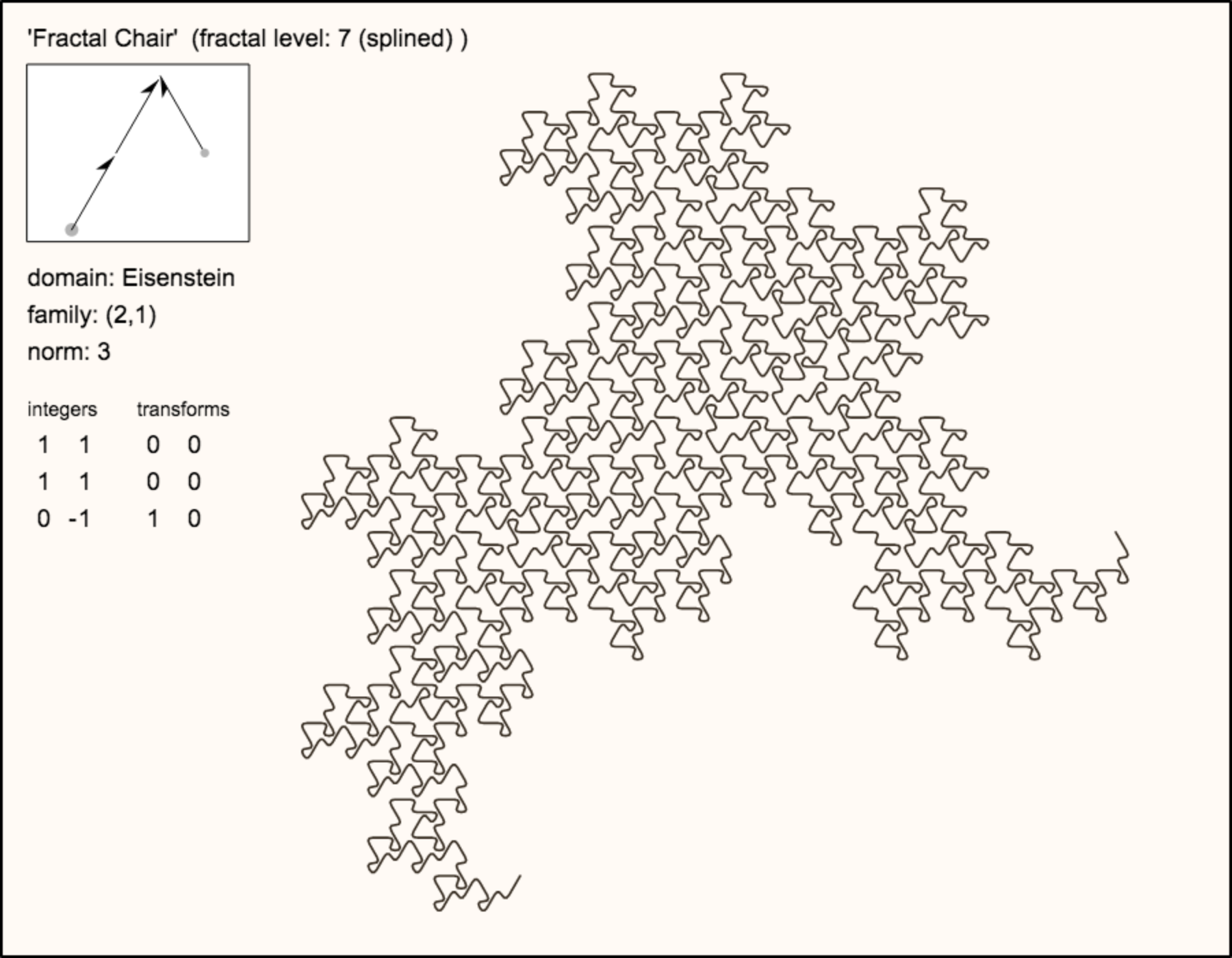
name: Fractal Chair reference: comment: Christoph Bandt

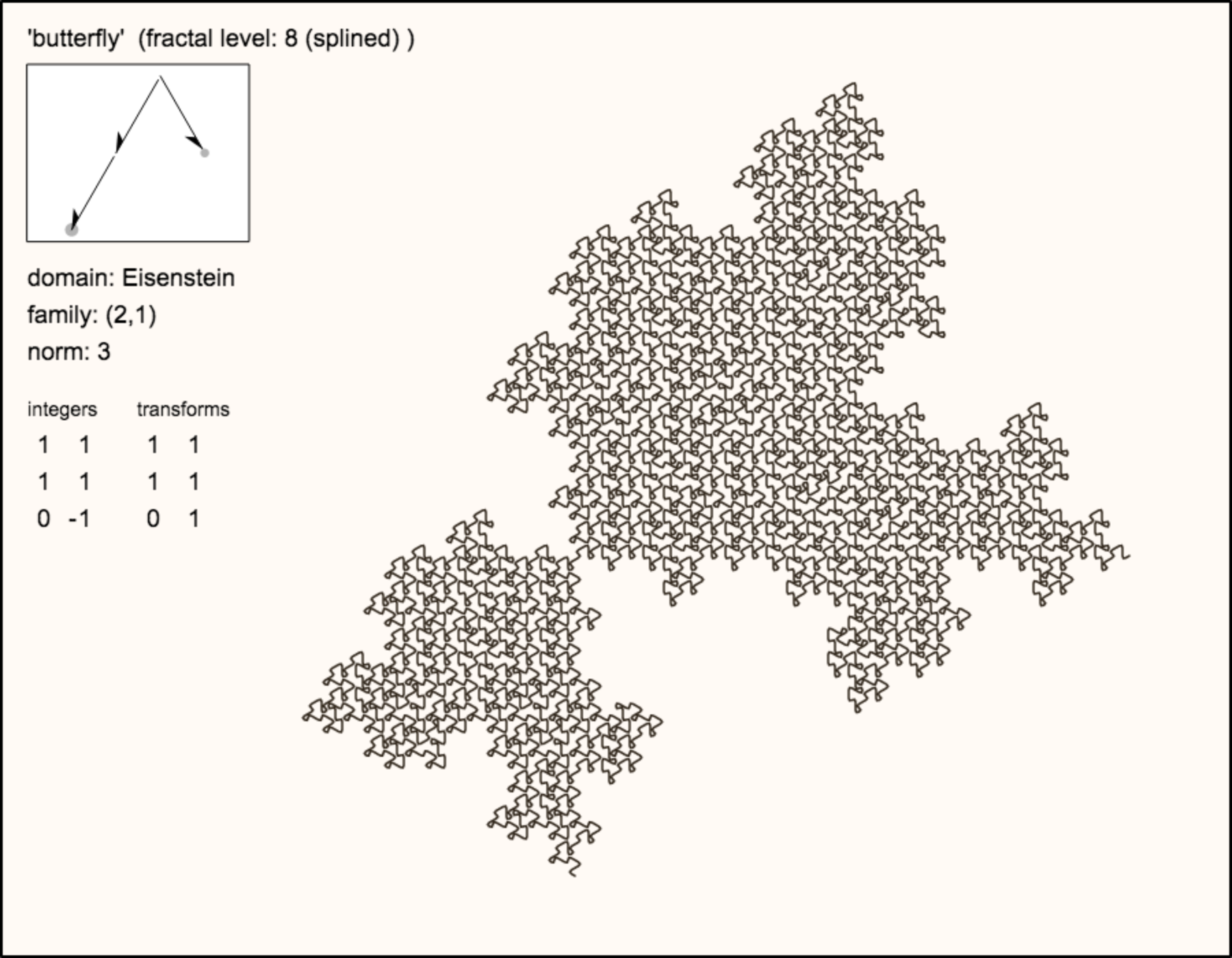
name: reference: comment:

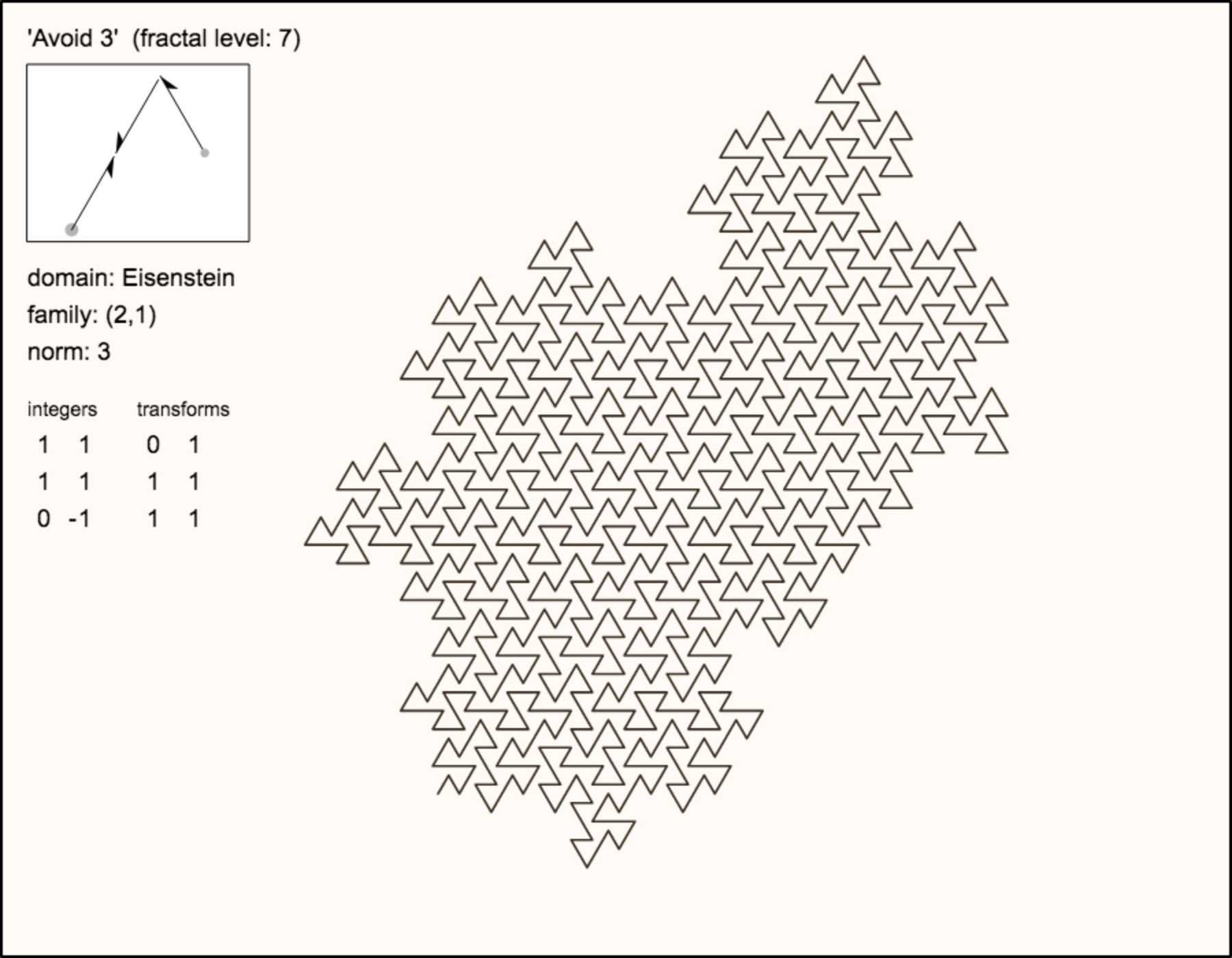
name: Avoid-3 reference: fractalcurves.com comment: This is a self-avoiding curve.

name: Hook 3 reference: fractalcurves.com comment:

name: Box 3 reference: The Family Tree of Fractal Curves comment: similar to the Original Peano Curve

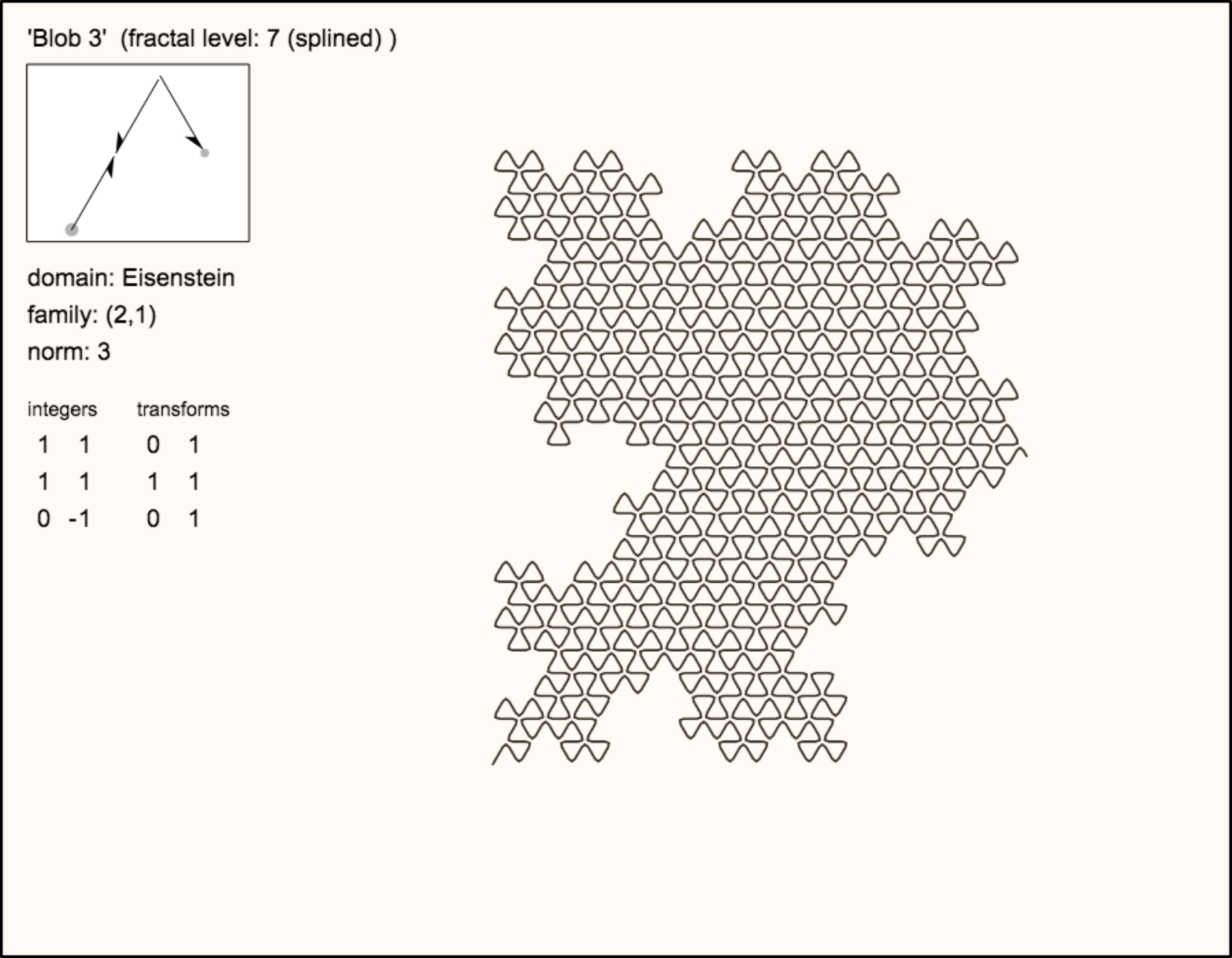
name: Blob 3 reference: fractalcurves.com comment:

fractalcurves.com