The Family Tree of Fractal Curves
describes a taxonomy of plane-filling curves
(2D space-filling curves)
using complex integers.
An earlier version of this taxonomy is described in
Brainfilling Curves.
This method is used to both classify and
generate plane-filling curves, including the classics:
the Original Peano curve,
the Dragon curve,
the Gosper curve,
the Snowflake sweep,
and several others. These classic curves were explained within a general framework in
Benoit Mandelbrot's book,
The Fractal Geometry of Nature.

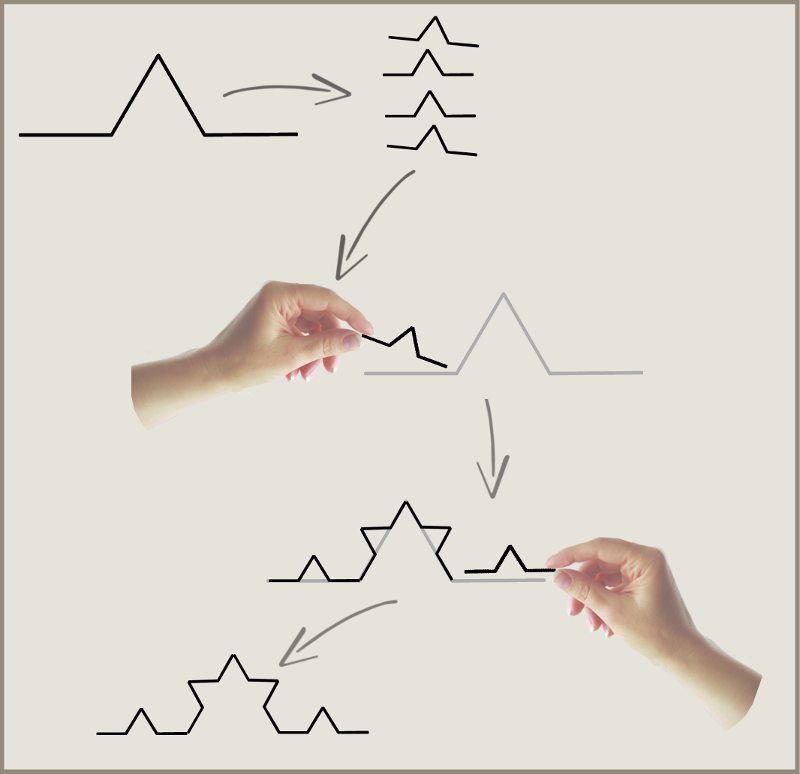
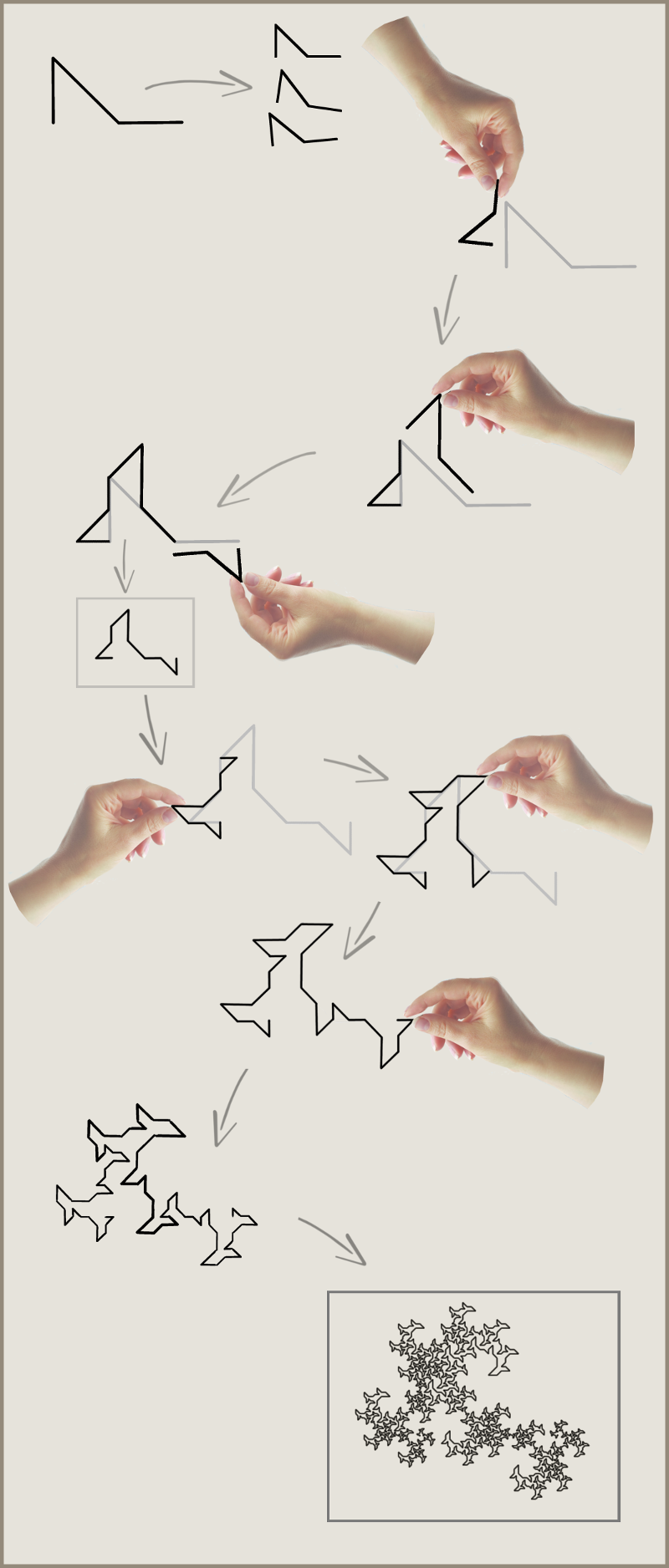
Plane-filling curves using edge-replacement (Koch-construction) are included in this archive.
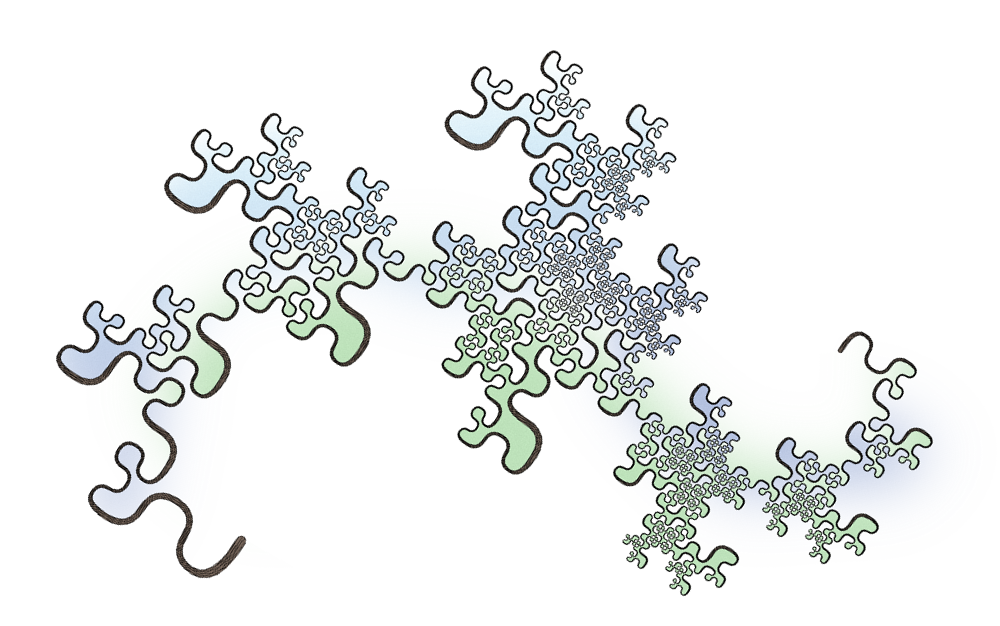
Each curve has a fractal dimension of 2.
Not all plane-filling curves are topologically equivalent to a disc: some curves have tremas (holes) or complex, self-contacting boundaries. However, all of them have regions that fill the plane locally. None of them are
gaskets.
Each family of plane-filling curves corresponds to a
Gaussian integer (square lattice) or an
Eisenstein integer (triangular lattice).
Any fractal generator can be described as an array of complex
integers - each of which corresponds
to one segment of the generator. The sum of these integers is the 'family integer'. The integers in any plane-filling curve generator sum to the family integer.
The reason a taxonomy is possible may have something to do with the iterative nature of genesis, and the presence of certain constraints that encourage structures to emerge. Like biological organisms, these constraints come into play when genotypes guide the expression of phenotypes through recursion. For these curves, the lattice of complex integers corresponds to some of those constraints. This book lays the foundations of a framework for categorizing self-similar, plane-filling fractal curves.
|
|




























